Правило из геометрии умножение десятичной дроби
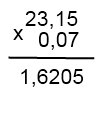
Оглавление:
- Как умножать десятичные дроби
- Действия с десятичными дробями
- Умножение десятичных дробей
- Умножение десятичных дробей
- Как умножить десятичную дробь на натуральное число
- Умножение десятичной дроби на натуральное число
- правила про умножения десятичных дробей напишите пж.
- Дроби. Умножение десятичных дробей.
Как умножать десятичные дроби
То есть фактически вместо умножения 36,85 на 1,14 мы умножаем 3685 на 14. Получаем 51590. Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе.
В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.
Чтобы умножить эти десятичные дроби, умножим числа, не обращая внимания на запятые.
То есть умножаем натуральные числа 2315 и 7. Получаем 16205. В этом числе нужно отделить после запятой четыре цифры — столько, сколько их в обоих множителях вместе (в каждом — по два). Окончательный ответ: 23,15∙0,07=1,6205.
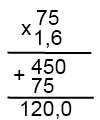
Умножение десятичной дроби на натуральное число выполняется аналогично.
Действия с десятичными дробями
Для этого опять же соблюдаем правило «запятая под запятой»: Получили ответ 8,5.
Значит выражения 3,2 + 5,3 равно 8,5 3,2 + 5,3 = 8,5 На самом деле, не всё так просто, как кажется на первый взгляд.
Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим. У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных.
При этом разряды начинаются после запятой. Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Умножение десятичных дробей
А если бы в условии задачи, не было ни каких величин и переводить было бы не чего, как тогда бы мы справились? В таких случаях используют правило умножения десятичных дробей. Для того чтобы найти произведение двух десятичных дробей, надо: 1) умножить их столбиком как целые числа, не обращая внимания на запятые.
2) После этого, в каждом множителе нужно посчитать количество знаков после запятой и сложить эти значения.
3) В полученном результате отделить запятой справа столько цифр, сколько их стоит в обоих множителях вместе. Задание Найти произведение чисел 3,143 и 1,5.
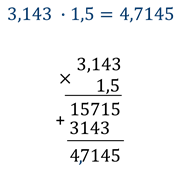
Как видите, в этом нет ничего сложного, если соблюдать правило умножения десятичных дробей.
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди дописывают нуль или несколько нулей.
Умножение десятичных дробей
В полученном результате следует отделить запятой две последние цифры: 142,70.
Так как нули после запятой в конце записи десятичной дроби не пишут, то 71,35∙2=142,70=142,7. 3) 0, 000836∙17=?

Умножаем, не принимая во внимание запятую: 836∙17=14212.
Итак, 0, 000836∙17=0 ,01412. 2. . Чтобы перемножить две десятичные дроби, нужно: перемножить числа, не обращая внимания на запятую; в полученном произведении отделить после запятой столько цифр, сколько их после запятых в обоих множителях вместе.
Как умножить десятичную дробь на натуральное число
52,783∙34=? Умножаем числа, отбросив запятую: 52783∙34=1794622.
Так как в записи десятичной дроби 52,783 после запятой стоит три цифры, в полученном произведении после запятой также должно стоять три цифры: 1794,622. Итак, 52,783∙34=1794,622. 5) 0,00078∙12=?

Умножение десятичной дроби на натуральное число заменяем умножением натуральных чисел: 78∙12=936.
Теперь нужно отделить после запятой столько цифр, сколько их после запятой в десятичной дроби 0,00078, то есть пять цифр: 0,00936.
В результате имеем: 0,00078∙12=0,00936.
Поскольку от перемены мест множителей произведение не меняется (), умножение числа на натуральную дробь проводят точно так же. Примеры. Выполнить умножение натуральных чисел на десятичные дроби: 1) 958∙0,007; 2) 31∙0,000046; Решение: 1) 958∙0,007=?
Умножение десятичной дроби на натуральное число
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
-
В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач. Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга. Воспитывать интерес к математике, активность, мобильность, умение общаться.
Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.
Объяснение
Все о десятичных дробях (2019)
раз, если перенести десятичную точку на одну, две, три и т.д.
4. Вычитание десятичных дробей. Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком» 5. Умножение десятичных дробей. Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа.
При умножении нам неважно, стоят ли запятые под запятыми и так далее. Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
правила про умножения десятичных дробей напишите пж.
деление десятичной дроби на 0,1 ; 0,01 ; 0,001 и т.д .
Прошу вас , помогите , заранее спасибо. 5-9 класс Вы находитесь на странице вопроса «», категории «математика».
Данный вопрос относится к разделу «5-9» классов. Здесь вы сможете получить ответ, а также обсудить вопрос с посетителями сайта. Автоматический умный поиск поможет найти похожие вопросы в категории «математика».
Если ваш вопрос отличается или ответы не подходят, вы можете задать новый вопрос, воспользовавшись кнопкой в верхней части сайта. Популярное Annacat777 / 03 июля 2016 г., 21:57:19 Vlad / 17 янв.
2021 г., 11:53:13 LILI8989 / 01 окт. 2016 г., 20:25:31 Pantush2000 / 22 апр. 2016 г., 11:12:09 ОляЛойко / 23 дек.
2015 г., 20:14:33 Катя25683 / 13 марта 2017 г., 8:16:37 Superdavid / 03 дек. 2014 г., 9:32:14 Maks00721 / 21 мая 2013 г., 13:30:22 Marysoldier / 01 дек.
Дроби. Умножение десятичных дробей.
Умножение производят в 3 этапа: 1. Десятичные дроби записываются в столбик и как обычные числа.
2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем. 3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.
1. Умножить, не обращая внимания на запятую.
2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе. Умножая десятичную дробь на натуральное число, необходимо: 1. Умножить числа, не обращая внимания на запятую; 2.
В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.
Рассмотрим на примере: Записываем десятичные дроби в столбик и умножаем их как , не обращая внимания на запятые. Т.е. 3,11 мы рассматриваем как 311, а 0,01 как 1. Результатом является 311. Далее считаем число знаков (цифр) после запятой у обеих дробей.
В 1-ой десятичной 2 знака и во 2-рой — 2.
Общее число цифр после запятых: 2 + 2 = 4 Отсчитываем справа налево четыре знака у результата. В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.
В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль. Обратите внимание: Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.